證明：如果兩個(gè)三角形有兩條邊和其中一邊上的中線對(duì)應(yīng)相等,，那么這兩個(gè)三角形全等（提示：先分清已知和求證,，然后畫出圖形，在結(jié)合圖形用數(shù)學(xué)符號(hào)表示已知和求證．）
題目
可圈可點(diǎn)用戶
2021-03-23 14:23
優(yōu)質(zhì)解答
答案
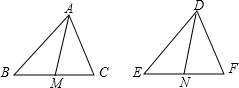
已知：△ABC和△DEF中,，AB=DE，BC=EF,，AM是△ABC的中線,，DN是△DEF的中線,，AM=DN，
求證：△ABC≌△DEF．
證明：∵BC=EF,，AM是△ABC的中線,，DN是△DEF的中線,，
∴BM=EN，
在△ABM和△DEN中,，
∵AB=DEBM=ENAM=DN ,，
∴△ABM≌△DEN（SSS），
∴∠B=∠E,，
在△ABC和△DEF中，
∵AB=DE∠B=∠EBC=EF,，
∴△ABC≌△DEF（SAS）．
查看答案
可圈可點(diǎn)用戶
2021-03-23 19:23
相關(guān)題庫(kù)
下載試題
復(fù)制試題
最新題庫(kù)
奇數(shù)中最小的合數(shù)是幾
2021-03-23
已知甲=2×2×3，乙=2×3×5
2021-03-23
密度的國(guó)際單位
2021-03-23
12和18的最小公倍數(shù)
2021-03-23
美國(guó)本土西臨什么洋
2021-03-23
美國(guó)的硅谷位于
2021-03-23
“硅谷”位于哪里
2021-03-23
根吸收水分和無(wú)機(jī)鹽的最主要的部位是
2021-03-23
艾滋病主要傳播的途徑v
2021-03-23
熱門題庫(kù)
下列食品中含碘量最少的是什么
2021-03-16
中國(guó)第一個(gè)共產(chǎn)黨早期組織是在哪里成立
2021-03-17
我國(guó)旱澇災(zāi)害多的主要原因是
2021-03-21
什么的楓葉填合適詞語(yǔ)
2021-03-17
中國(guó)共產(chǎn)黨和各民主黨派的關(guān)系是
2021-03-22
下列山脈屬于我國(guó)第一階梯和第二階梯的界線的是
2021-03-17
大躍進(jìn)運(yùn)動(dòng)的主要標(biāo)志是
2021-03-17
新三民主義與舊三民主義相比較
2021-03-15
where are you going
2021-03-23
最新資訊
高職高考可以報(bào)考哪些大學(xué) 3+證書可以考哪些大學(xué)
2021-04-02
教資出成績(jī)2021 教資出成績(jī)了嗎
2021-04-02
重慶2021高職分類考試招生公布 重慶高職分類考試招生計(jì)劃
2021-04-02
財(cái)政部招人需要什么專業(yè) 財(cái)政部怎么招人
2021-04-02
成考本科需要什么學(xué)歷 第二學(xué)歷和第一學(xué)歷有什么區(qū)別
2021-04-01
初中生厭學(xué)怎么解決 初中生不想讀書了怎么辦
2021-04-01
熱門資訊
教育改革2021最新消息 2021年教育改革內(nèi)容
2021-03-18
高考志愿填報(bào)技巧與指南2021 2021高考志愿填報(bào)指南
2021-03-19
四川大學(xué)華西臨床醫(yī)學(xué)院錄取分?jǐn)?shù)線2020
2021-03-15
2021北京沙塵暴原因 北京沙塵暴的原因是什么
2021-03-19
中考分流政策2021 中考分流是什么意思
2021-03-16
上海學(xué)區(qū)房新政策2021 上海學(xué)區(qū)房改革最新消息
2021-03-17
查看答案
限時(shí)優(yōu)惠:
00時(shí)00分00秒
熱門
單次付費(fèi)有效 3.99 元
用于查看答案,，單次有效 19.99元
微信掃碼支付
包月VIP 9.99 元
用于查看答案，包月VIP無(wú)限次 49.99元
登錄后掃碼支付
微信掃碼支付
去登陸