
已知函數(shù)f(x)=x(1-lnx)
(1)討論f(x)的單調(diào)性
(2)設(shè)a,b為兩個(gè)不相等的正數(shù),且blna-alnb=a-b證明: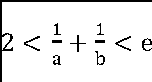


已知函數(shù)f(x)=x(1-lnx)
(1)討論f(x)的單調(diào)性
(2)設(shè)a,b為兩個(gè)不相等的正數(shù),且blna-alnb=a-b證明: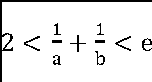

答案



擴(kuò)展知識(shí)
函數(shù)的單調(diào)性(monotonicity)也叫函數(shù)的增減性,可以定性描述在一個(gè)指定區(qū)間內(nèi),函數(shù)值變化與自變量變化的關(guān)系,。當(dāng)函數(shù)f(x) 的自變量在其定義區(qū)間內(nèi)增大(或減?。r(shí),函數(shù)值也隨著增大(或減?。?,則稱該函數(shù)為在該區(qū)間上具有單調(diào)性(單調(diào)遞增或單調(diào)遞減) [1] 。在集合論中,,在有序集合之間的函數(shù),,如果它們保持給定的次序,是具有單調(diào)性的,。
如果說明一個(gè)函數(shù)在某個(gè)區(qū)間D上具有單調(diào)性,,則我們將D稱作函數(shù)的一個(gè)單調(diào)區(qū)間,則可判斷出:
D?Q(Q是函數(shù)的定義域),。
區(qū)間D上,,對(duì)于函數(shù)f(x),?(任取值)x1,,x2∈D且x1>x2,,都有f(x1) >f(x2)?;?,? x1,x2∈D且x1>x2,,都有f(x1) <f(x2),。
函數(shù)圖像一定是上升或下降的。
該函數(shù)在E?D上與D上具有相同的單調(diào)性,。
注意:函數(shù)單調(diào)性是針對(duì)某一個(gè)區(qū)間而言的,,是一個(gè)局部性質(zhì)。因此,,說單調(diào)性時(shí)最好指明區(qū)間,。
有些函數(shù)在整個(gè)定義域內(nèi)是單調(diào)的;有些函數(shù)在定義域內(nèi)的部分區(qū)間上是增函數(shù),,在部分區(qū)間上是減函數(shù),;有些函數(shù)是非單調(diào)函數(shù),如常數(shù)函數(shù),。
函數(shù)的單調(diào)性是函數(shù)在一個(gè)單調(diào)區(qū)間上的“整體”性質(zhì),,具有任意性,不能用特殊值代替,。
在利用導(dǎo)數(shù)討論函數(shù)的單調(diào)區(qū)間時(shí),,首先要確定函數(shù)的定義域,解決問題的過程中只能在定義域內(nèi),通過討論導(dǎo)數(shù)的符號(hào)來判斷函數(shù)的單調(diào)區(qū)間,。
如果一個(gè)函數(shù)具有相同單調(diào)性的單調(diào)區(qū)間不止一個(gè),,那么這些單調(diào)區(qū)間不能用“∪”連接,而只能用“逗號(hào)”或“和”字隔開,。
查看答案
單次付費(fèi)有效 3.99 元
用于查看答案,單次有效 19.99元
包月VIP 9.99 元
用于查看答案,,包月VIP無限次 49.99元